Table of Contents
Overview
Composite numbers are defined as numbers with more than two factors. Non-prime numbers are composite numbers because they can be divided by more than two numbers.
Example: 4 has more than two factors i.e. 1, 2, and 4. So 4 is a composite number.
Types of Composite Numbers
There are two types of Composite Numbers:
1. Odd composite numbers: They are those that have an odd digit in the unit’s place. In other words, odd composite numbers are all odd numbers that are not prime numbers.
For instance: 9, 15, 21, and so on.
2. Even composite numbers: They are those that have an even digit in the unit’s place. In other words, all even numbers other than 2 are even composite numbers. This is due to the fact that no even number (except 2) can ever be a prime number.
For instance: 8, 12, 14, and so on.
How to find Composite Numbers
To find a composite number, we must first find the factors of the given number. When a number has more than two factors, it is said to be composite.
The divisibility test is the best way to determine a composite number. The divisibility test can help us determine whether a number is prime or composite. Divisibility occurs when a number is completely divided (with no remainder) by a number other than 1 and itself.
To do so, we must first determine whether the number can be divided by the following common factors: 2, 3, 5, 7, 11, and 13. If the given number is an even number, begin checking with the number 2.
If the number ends in a 0 or a 5, multiply it by 5. If the number cannot be divided by any of these numbers, it is a prime number. For example, 68 is divisible by 2, indicating that it has factors other than 1 and 68; thus, 68 is a composite number.
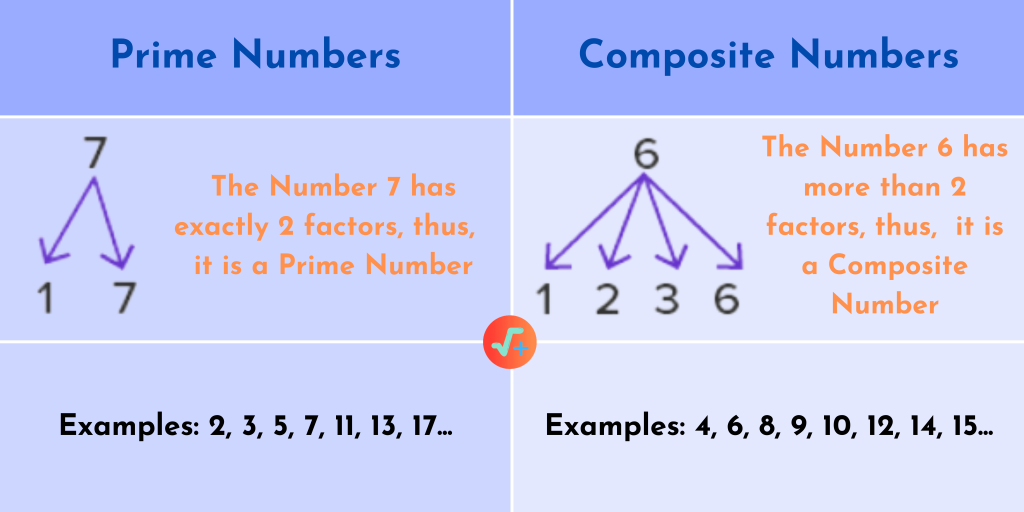
Difference between Prime and Composite Numbers
A composite number is one that is divisible by a number other than one and the number itself. This means that composite numbers contain more than two factors. For instance, 4 and 6 are composite numbers.
In contrast, a prime number is one that is divisible only by one and itself, such as 2, 3, and 5. This means that a prime number has only two factors: 1 and the number itself.
Video Explanation
Other Maths concepts
To understand maths concepts, please check our other articles:
- Rational and Irrational Numbers Easy Concepts – Class 9 Chapter 1
- What are Natural Numbers
- Integers Definition With Easy Examples | What Are Integers
- Whole Numbers | Definition, Examples, Full Explanation
- Imaginary Numbers Definition With Easy Examples
- Real Numbers Definition | Real Numbers Examples
FAQ
Q.1. Is 0 a composite number?
Ans. The number zero is neither prime nor composite. Because any number multiplied by zero equals zero, a product of zero has an infinite number of factors. A composite number must have a set of factors.
Q.2. Why 1 is not a composite?
Ans. A composite number is a natural number with more than two positive factors. However, 1 has only one factor, which is itself. As a result, one is not a composite number.
Q.3. Which is the smallest composite number?
Ans. 4 is the smallest composite number.
Q.4. Which is the largest four-digit composite number?
Ans. The largest four-digit number is 9999, which is also divisible by “3”, making 9999 the largest composite number.
Q.5. What are prime and composite numbers?
Ans. A prime number is one with exactly two factors, namely ‘1’ and the number itself. A composite number has more than two factors, which means that it can be divided by at least one positive integer in addition to 1 and the number itself.
Q.6. What are the composite numbers from 1 to 100?
Ans. The list of composite numbers from 1 to 100 are:
4, 6, 8, 9, 10, 12, 14, 15, 16, 18, 20, 21, 22, 24, 25, 26, 27, 28, 30, 32, 33, 34, 35, 36, 38, 39, 40, 42, 44, 45, 46, 48, 49, 50, 51, 52, 54, 55, 56, 57, 58, 60, 62, 63, 64, 65, 66, 68, 69, 70, 72, 74, 75, 76, 77, 78, 80, 81,82, 84, 85, 86, 87, 88, 90, 91, 92, 93, 94, 95, 96, 98, 99, 100.