Table of Contents
Overview
There are 9 questions in Class 9 Maths Exercise 1.3. The questions and their solutions with examples are explained in easy language.
Question/Answers
| S.No. | Question & Answer |
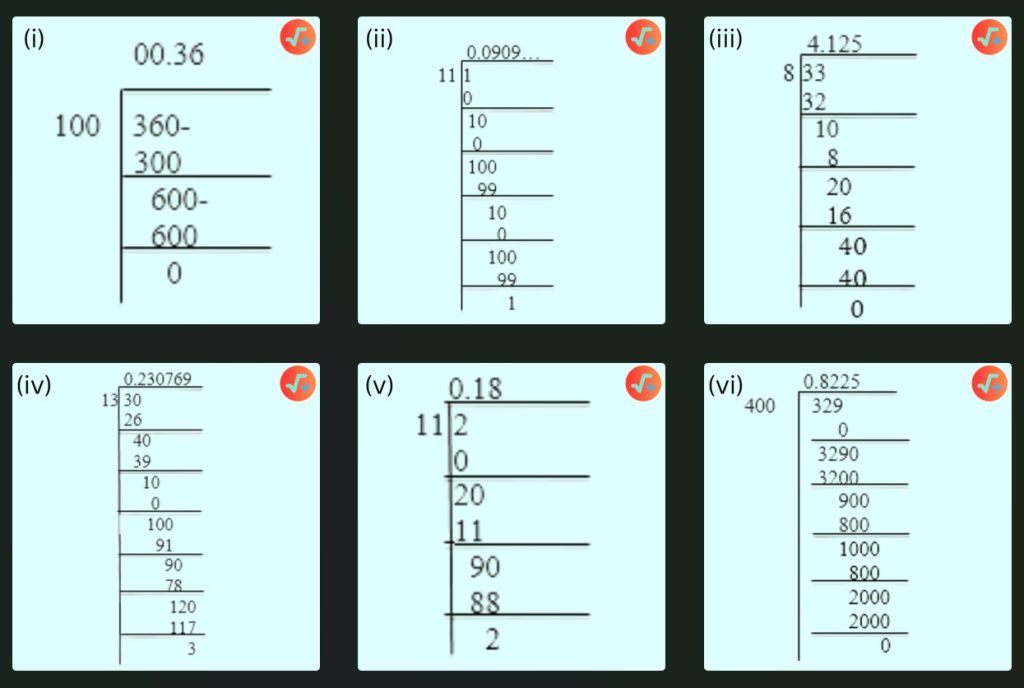
| Q.1. | Write the following in decimal form and say what kind of decimal expansion each has: (i) 36/100 (ii) 1/11 (iii) 4⅛ (iv) 3/13 (v) 2/11 (vi) 329/400 |
| Ans. | (i) 0.36, Terminating (ii) 0.09…, Non Terminating (iii) 33/8= 4.125, Terminating (iv) 0.230769…, Non Terminating (v) 0.18…, Non Terminating (vi) 0.8225, Terminating |
| Q.2. | You know that 1/7 = 0.142857… Can you predict what the decimal expansions of 2/7, 3/7, 4/7, 5/7, 6/7 are, without actually doing the long division? If so, how? (Hint: Study the remainders while finding the value of 1/7 carefully.) |
| Ans. | 1/7= 0.142857… so 2/7= 2×1/7= 2x 0.142857…= 0.285714… 3/7= 3×1/7= 3x 0.142857…= 0.428571… 4/7= 4×1/7= 4x 0.142857…= 0.571428… 5/7= 5×1/7= 5x 0.142857…= 0.714285… 6/7= 6×1/7= 6x 0.142857…= 0.857142… |
| Q.3. | Express the following in the form p/q, where p and q are integers and q ≠0. (i) 0.6… (ii) 0.47… (iii) 0.001… |
| Ans. | (i) 0.6…= 0.666 Let x = 0.666… Then, 10x = 6.666… 10x = 6+0.666 10x = 6 + x 9x = 6 x=6/9 x = 2/3 (which is=0.6…) (ii) 0.47…= 0.477 Let x= 0.477… Then, 10x=4.777 10x-x= 4.777-0.477 9x=4.3 x=4.3/9 x=43/90 (which is =0.477…) (iii) Let x= 0.001… Then, 10x= 0.011 10x-x= 0.011-0.001 9x=0.01 x= 0.01/9 x= 1/900 (which is =0.001…) |
| Q.4. | Express 0.99999…. in the form p/q . Are you surprised by your answer? With your teacher and classmates discuss why the answer makes sense. |
| Ans. | Let x= 0.9999… 10x= 9.999 10x-x= 9.999-0.999 9x= 9 x=9/9 x=1 The difference between 1 and 0.999999 is 0.000001, which is negligible. As a result, we can conclude that 0.999 is too close to 1, and 1 as the answer is justified. |
| Q.5. | What can the maximum number of digits be in the repeating block of digits in the decimal expansion of 1/17 ? Perform the division to check your answer. |
| Ans. | The repeating block of the decimal expansion of 1/17 has 16 digits. The image shows the complete answer. |

| Q.6. | Look at several examples of rational numbers in the form p/q (q ≠ 0), where p and q are integers with no common factors other than 1 and having terminating decimal representations (expansions). Can you guess what property q must satisfy? |
| Ans. | When q is 2, 4, 5, 8, 10… The decimal expansion is then completed. As an example, 1/2=0.5, denominator q = 2¹ 7/8 = 0. 875, denominator q = 2³ 4/5=0.8, Denominator q = 5¹ We can see that the terminating decimal can be obtained when the prime factorization of the given fractions denominators has the power of only 2 or 5 or both. |
| Q.7. | Write three numbers whose decimal expansions are non-terminating non-recurring. |
| Ans. | Non-terminating non-recurring decimal is a number with an infinite number of digits after the decimal point and no pattern of digit repetition. Irrational numbers are non-terminating non-recurring decimals. Examples: √2 = 1.414213562 ……….. √3 = 1.732050808 ……. √5 = 2.23606797 ……. |
| Q.8. | Find three different irrational numbers between the rational numbers 5/7 and 9/11 . |
| Ans. | Let’s use the long division method to find the decimal expansion of 5/7 and 9/11. |

| We can write 3 irrational numbers between 5/7 and 9/11 as: (i) 0.721722172221 . . . (ii) 0.750975009750009 . . . (iii) 0.808008000 . . . | |
| Q.9. | Classify the following numbers as rational or irrational: (i) √23 (ii) √225 (iii) 0.3796 (iv) 7.478478 (v) 1.101001000100001… |
| Ans. | (i) √23 = √23/1 = p/q but here p is not an integer so √23 is an irrational number. (ii) √225 = 15/1, where p and q are integers and q≠ 0 so √225 is a rational number. (iii) 0.3796 Because 0.3796 is a terminating decimal number, it is a rational number. (iv) 7.478478 is a rational number because it is a non-terminating recurring decimal, i.e. the number block 478 repeats. (v) 1.101001000100001… Because it is a non-terminating and non-recurring decimal, it is an irrational number. |
Video Explanation
Maths Concepts
To understand maths concepts of Rational numbers, Integers, etc used in NCERT Class 9 Maths Exercise 1.3, please also check the following articles: