Table of Contents
Overview
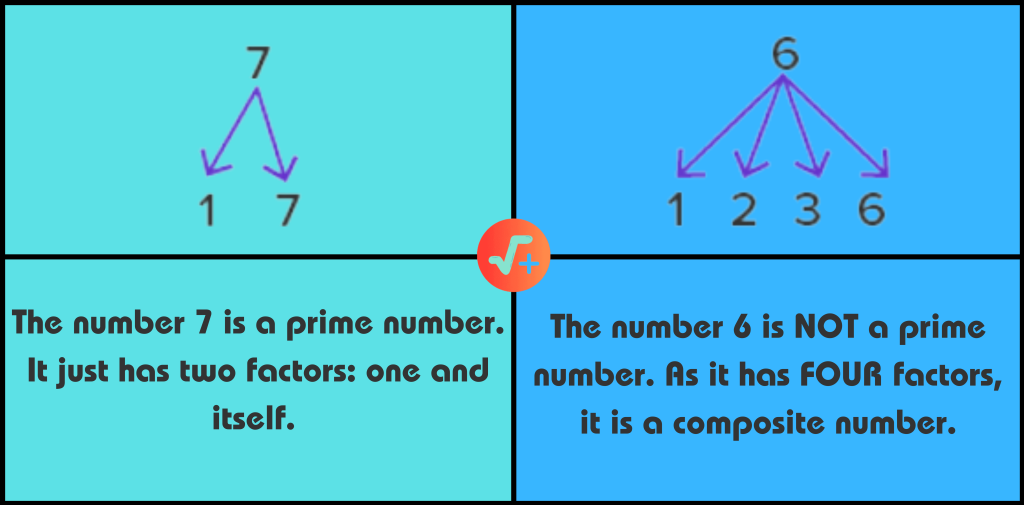
Prime numbers are those that are greater than 1. They have exactly two factors, 1 and the number itself. This means that these numbers cannot be divided by any number other than 1 and the number itself. Some examples of Prime Numbers are 7, 31, 83, 239, 953.
The number 39 is the product of two prime numbers (3 and 13).
Examples and Non-Examples of Prime Numbers
Types of Prime Numbers
There are two types of prime numbers:
1. Odd Prime Numbers
2. Even Prime Numbers
Except for the number 2, which is an even number, all prime numbers are odd. Surprisingly, 2 is the only prime number that is even. This means that the list of odd numbers can begin with 3 and continue indefinitely because the remaining prime numbers are odd numbers. 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, and so on are examples of odd prime numbers.
How to find Prime Numbers
There are several methods for determining prime numbers. Let’s take a look at one of these methods.
Method: Except for 2 and 3, every prime number can be written as ‘6n + 1 or 6n – 1’.
So, if we have a number other than 2 or 3, we can determine whether it is prime or not by attempting to express it in the form of 6n + 1 or 6n – 1.
Check out this formula: 6n – 1 for the number 1. So, 6(1) – 1 = 5
Check out this formula: 6n + 1 for the number 1, which equals 6(1) + 1 = 7.
Check out this formula, 6n – 1, for the number 2, So, 6(2) – 1 = 11
Check out this formula, 6n + 1, for the number 2, So, 6(2) +1 = 13.
Now by this way, we know numbers 5, 7, 11, and 13 are prime numbers.
Video Explanation
Other Maths Concepts
To understand maths concepts, please check our other articles:
- Rational and Irrational Numbers Easy Concepts – Class 9 Chapter 1
- What are Natural Numbers
- Integers Definition With Easy Examples | What Are Integers
- Whole Numbers | Definition, Examples, Full Explanation
- Imaginary Numbers Definition With Easy Examples
- Real Numbers Definition | Real Numbers Examples
FAQ
Q1. What are the 10 first prime numbers?
Ans. The first ten prime numbers are 2, 3, 5, 7, 11, 13, 17, 19, 23, and 29. It should be noted that 1 is not a prime number.
Q2. Why prime numbers are called so?
Ans. They are “prime” in the sense that they “come first”, in that we can acquire all of the others (composite numbers) by multiplying them together.
Q3. Is 1 a prime Number?
Ans. The number “1” is neither prime nor composite.
Q4. Is 0 a prime Number
Ans. Zero is neither a composite nor a prime. A product of zero can have an infinite number of factors because zero times any number equals zero.
Q5. What are Prime Numbers?
Ans. A whole number greater than one that cannot be divided exactly by any whole number other than itself and 1 (for example, 2, 3, 5, 7, 11).
Q6. What are Prime Numbers between 1 and 100?
Ans. 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97
Q7. What is the smallest Prime Number?
Ans. 2 is the smallest prime number. Also, 2 is the only prime number that is even.