Table of Contents
Overview
There are 5 questions in Class 9 Maths Exercise 1.4. The questions and their solutions with examples are explained in easy language.
Question/Answers
| S.No. | Question & Answer |
| Q.1. | Classify the following numbers as rational or irrational. (i) 2-√5 (ii) (3+√23)-√23 (iii) 2√7/7√7 (iv) 1/√2 (v) 2π |
| Ans. | (i) Since, it is the difference between a rational and an irrational number. ∴2 -√5 is an irrational number. (ii) (3+√23)-√23 = 3+√23-√23 =3, which is a rational number. (iii) 2√7/7√7 = 2/7, which is a rational number. (iv) Since the quotient of a rational and an irrational number is an irrational number. ∴1/√2 is an irrational number. (v) Since the product of a rational and an irrational number is an irrational number. ∴2π is an irrational number. |
| Q.2. | Simplify each of the following expressions: (i) (3+√3)(2+√2) (ii) (3+√3)(3-√3) (iii) (√5+√2)² (iv) (√5-√2)(√5+√2) |
| Ans. | (i) (3+√3)(2+√2) = 3(2+√2)+√3(2+√2) = 6+3√2+2√3+√6 (ii) (3+√3)(3-√3) = 3(3-√3) +√3(3-√3) =9-3√3+3√3-√9 =9-3 =6 (iii) (√5+√2)² (using (√a+√b)²= a+2√ab+b) =(√5)2 + (√2)2 + 2(√5)(√2) = 5 + 2 + 2√10 = 7 + 2√10 (iv) (√5-√2)(√5+√2) (using (a+b)(a-b)= a2–b2 ) =(√5)2 – (√2)2 = 5 – 2 = 3 |
| Q.3. | Recall, π is defined as the ratio of the circumference (say c) of a circle to its diameter (say d). That is π = c/d. This seems to contradict the fact that π is irrational. How will you resolve this contradiction? |
| Ans. | Remember that when we measure the length of a line with a scale or another device, we only get an approximate rational value, i.e. c and d are both irrational. c/d is irrational and thus π is irrational. As a result, there is no contradiction in claiming that it is irrational. |
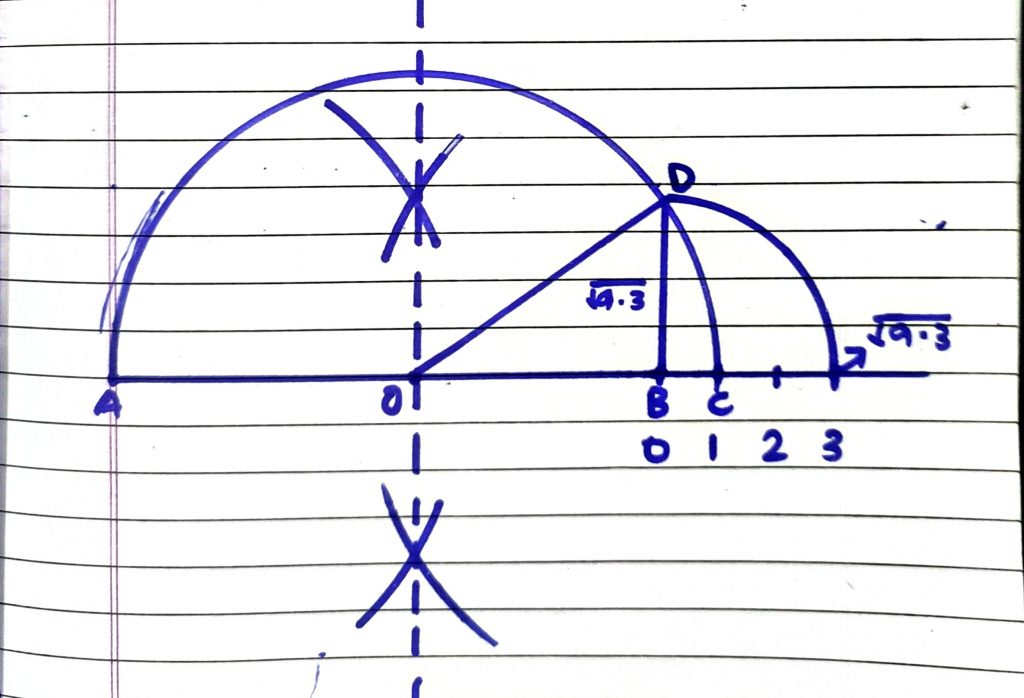
| Q.4. | Represent √9.3 on the number line. |
| Ans. | Let AB=x AC=x+1 OA=OC=(x+1)/2 OB=OC-1 =(x+1)/2 -1 =(x-1)/2 In △BOD, BD2 = OD2 -OB2 = {(x+1)/2}2 – {(x-1)/2}2 = (x2 +1+2x-x2 -1+2x)/4 = 4x/4 BD2= x ∴BD= √x =√9.3 (as x=9.3) |
| Q.5. | Rationalize the denominators of the following: (i) 1/√7 (ii) 1/(√7-√6) (iii)1/(√5+√2) (iv) 1/(√7-2) |
| Ans. |

Video Explanation
Other Maths Concepts
To understand maths concepts of Rational numbers, Integers, etc used in NCERT Class 9 Maths Exercise 1.4, please also check the following articles: